Java集合之Map——HashMap详解

发表于 | 分类于

Java集合之Map——HashMap详解

下文中哈希表由多个桶组成(Node<K,V> 为单个桶，哈希表定义为 Node<K,V>[ ] table)

每个元素存在桶中，桶中的存储结构可能只有单个元素，可能是链表连接的多个元素，也有可能是红黑树结构

哈希表容量为表中能够存储元素的个数

简介

  1. HashMap 基于哈希表的Map接口实现，是以 key-value 存储形式存在，即主要用来存放键值对
  2. HashMap 的实现不是同步的，这意味着它不是线程安全的
  3. HashMap 中的映射不是有序的(即存取顺序不一致)
  4. 实现结构是 数组+链表+红黑树

源码解读

继承关系

1
2
public class HashMap<K,V> extends AbstractMap<K,V>
    implements Map<K,V>, Cloneable, Serializable

结构图：
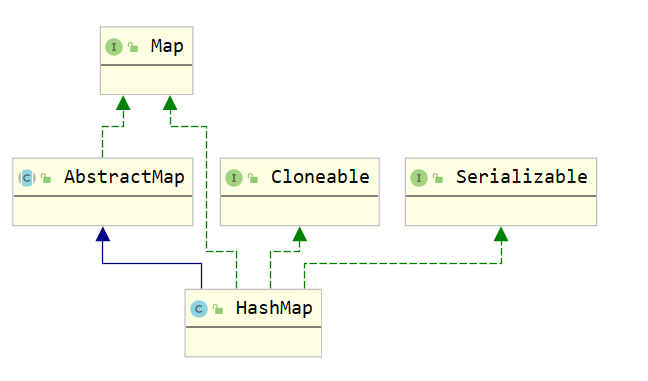
在这里插入图片描述

  • Cloneable 表示可以克隆，创建并返回HashMap对象的一个副本
  • Serializable 序列化接口，属于标记性接口，HashMap对象可以被序列化和反序列化
  • AbstractMap 父类提供了Map实现接口，以最大限度地减少实现此接口所需的工作

成员变量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
// 默认容量16，即桶的个数
static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; 
 
// 最大容量
static final int MAXIMUM_CAPACITY = 1 << 30;    
 
// 默认负载因子0.75
static final float DEFAULT_LOAD_FACTOR = 0.75f; 
 
// 链表节点转换红黑树节点的阈值, 9个节点转
static final int TREEIFY_THRESHOLD = 8; 
 
// 红黑树节点转换链表节点的阈值, 6个节点转
static final int UNTREEIFY_THRESHOLD = 6;   
 
// 转红黑树时table的最小长度，即转红黑树时桶的最小个数
static final int MIN_TREEIFY_CAPACITY = 64; 
 
//哈希表，多个哈希桶组成
transient Node<K,V>[] table;

//存储键值对的集合
transient Set<Map.Entry<K,V>> entrySet;

//哈希表的容量，可容纳元素个数，也称为阈值，为哈希表扩容的临界条件
int threshold;

//加载因子
final float loadFactor;

这里主要解释一下变量间的关系。

  1. threshold 是哈希表能存储的元素个数，也称为阈值，当表中存储元素个数大于阈值时，将会对哈希表进行扩容，即增加桶的个数，由 哈希桶数量乘以负载因子 决定；
  2. 源码中出现的capacity代表的是哈希表的大小，即表中哈希桶的个数，table.length，它与阈值不同；
  3. loadFactor，加载因子，也称负载因子，它表示HashMap的疏密程度，是阈值与哈希桶个数的比值，$loadFactor=\frac{threshold}{table.length}$，实时加载因子为$loadFactor=\frac{size}{table.length}$；
  4. TREEIFY_THRESHOLD，链表节点转换红黑树节点的阈值，当发生哈希冲突时，即两个以上的键值对的键的哈希值相同，他们会存储在同一个哈希桶下，它们起初是连接成一个链表，但是当节点个数不断增多时，整个哈希表的效率不断降低，当链表程度达到一定个数之后，会将其转化成红黑树的结构以此加快整体效率，默认阈值为8，即当链表程度为9时进行转换；
  5. UNTREEIFY_THRESHOLD，红黑树节点转换链表节点的阈值，与4中阈值含义相反，默认值为6；
  6. MIN_TREEIFY_CAPACITY，转红黑树时table的最小长度，默认值为64，在4的转换中有一点需要注意，当哈希桶的个数小于MIN_TREEIFY_CAPACITY时，链表长度达到9后不会直接转化成红黑树，而是会进行扩容，当桶的个数大于等于MIN_TREEIFY_CAPACITY= 64时，才会发生转换。

以上的一些值的设定的原因：

  1. 默认加载因子为什么为0.75？
    总结：是为了提高空间利用率和增加查询效率的折中，主要是泊松分布，0.75的话碰撞最小。
    首先当负载因子比较小时，阈值$threshold = table.length loadFactor$，所以哈希表能存的元素个数就更少，那么相应的发生哈希冲突的概率也就降低了，所以查询效率也就提高，但是相应的，增加相同数量的元素，需要的哈希桶的个数也就增加，也就增加了扩容方法（速度很慢）的调用次数，此情况下空间利用率也降低，所以不难发现查询效率和空间利用率是相互矛盾的，所以加载因子需要在时间和空间成本上寻求一种折中，而*0.75则是一种比较理想的取值。

  2. 为什么Map桶中节点个数超过8才转为红黑树？
    首先我们已经知道将链表转换成红黑树是为了加快查询效率，但是也带来了一些问题：
    （1）树节点的大小大约是普通节点的两倍，这就带来了空间的浪费；
    （2）在节点数量较低时，维护红黑树结构的成本是不低于查询成本的，所以此时不值得进行转换。
    综上我们不难看出这其实空间和时间的权衡，根据源码中的如下注释：

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    * Because TreeNodes are about twice the size of regular nodes, we
    * use them only when bins contain enough nodes to warrant use
    * (see TREEIFY_THRESHOLD). And when they become too small (due to
    * removal or resizing) they are converted back to plain bins.  In
    * usages with well-distributed user hashCodes, tree bins are
    * rarely used.  Ideally, under random hashCodes, the frequency of
    * nodes in bins follows a Poisson distribution
    * (http://en.wikipedia.org/wiki/Poisson_distribution) with a
    * parameter of about 0.5 on average for the default resizing
    * threshold of 0.75, although with a large variance because of
    * resizing granularity. Ignoring variance, the expected
    * occurrences of list size k are (exp(-0.5) * pow(0.5, k) /
    * factorial(k)). The first values are:
    *
    * 0:    0.60653066
    * 1:    0.30326533
    * 2:    0.07581633
    * 3:    0.01263606
    * 4:    0.00157952
    * 5:    0.00015795
    * 6:    0.00001316
    * 7:    0.00000094
    * 8:    0.00000006
    * more: less than 1 in ten million

    先解释一下是什么意思：在使用分布良好的hashcode时，很少使用红黑树结构，理想情况下，在随机哈希码下，箱子中节点的频率服从泊松分布，从上数最后的概率值不难看出，一个哈希桶中链表长度达到8个元素的概率为0.00000006，这几乎是一个不可能事件。所以，选择8，不是随便决定的，而是根据概率统计决定的。

构造方法

  1. public HashMap();，构造一个空的 HashMap ，默认初始容量（16）和默认加载因子（0.75）；（经常使用）
  2. public HashMap(int initialCapacity);，构造一个具有指定的初始容量和默认加载因子（0.75） HashMap；（推荐使用）
  3. public HashMap(int initialCapacity, float loadFactor);，构造一个具有指定的初始容量和加载因子的 HashMap；（不建议修改加载因子）
  4. HashMap(Map<? extends K,? extends V> m);，构造一个新的 HashMap与指定的相同的映射 Map 。

由于推荐使用的第二个构造方法中也是调用第三个构造方法，所以这里主要分析一下第三个构造方法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public HashMap(int initialCapacity, float loadFactor) {
	//对initialCapacity进行数据可行性处理
	if (initialCapacity < 0)
	    throw new IllegalArgumentException("Illegal initial capacity: " +
	                                       initialCapacity);
	//判断初始化容量initialCapacity是否大于集合的最大容量
	//MAXIMUM_CAPACITY，2^30，如果是则用最大容量替换设定容量
	if (initialCapacity > MAXIMUM_CAPACITY)
	    initialCapacity = MAXIMUM_CAPACITY;
	//对loadFactor进行数据可行性处理
	if (loadFactor <= 0 || Float.isNaN(loadFactor))
	    throw new IllegalArgumentException("Illegal load factor: " +
	                                       loadFactor);
	this.loadFactor = loadFactor;
	this.threshold = tableSizeFor(initialCapacity);
}

首先对于最后一行代码this.threshold = tableSizeFor(initialCapacity);，会觉得有一些问题，这里初始化的是哈希桶的数量，为什么会存储在阈值threshold中？对于上述所有成员变量，没有发现描述当前桶的个数的变量，但是可以通过table.length来获取，初始化时table = null，之后的复制和阈值的修正是在resize()即扩容方法中，下文有细讲。

再展开分析一下tableSizeFor(initialCapacity)函数，它返回一个不小于initialCapacity的最小2的次幂，为什么是2的次幂，在下面的分析中有细讲，这里主要讲一下这个函数：

  1. 为什么要对cap做减1操作：这是为了防止cap已经是2的幂。如果cap已经是2的幂， 又没有执行这个减1操作，则执行完后面的几条无符号右移操作之后，返回的capacity将是这个cap的2倍。
  2. 由于是移位后做|运算，所以过程有点像1的向左移位。
1
2
3
4
5
6
7
8
9
static final int tableSizeFor(int cap) {
	int n = cap - 1;
	n |= n >>> 1;
	n |= n >>> 2;
	n |= n >>> 4;
	n |= n >>> 8;
	n |= n >>> 16;
	return (n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;
}

这里通过一个例子来分析：
假设输入的cap = 10，即

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int n = cap - 1;//cap=10  n=9
n |= n >>> 1;
	00000000 00000000 00000000 00001001 //9
	00000000 00000000 00000000 00000100 //9 >>> 1 = 4
-------------------------------------------------
	00000000 00000000 00000000 00001101 //9 | (9 >>> 1) = 13
	
 n |= n >>> 2;//n = 13
	00000000 00000000 00000000 00001101  //13
    00000000 00000000 00000000 00000011  //13 >>> 2 = 3
-------------------------------------------------
	00000000 00000000 00000000 00001111 //13 | (13 >>> 2) = 15
接下去的移位也是类似，移4位、8位、16位，保证在2 ^ 30内能达到目标即可
此时已经得到我们想要的结果，所以就不继续下去了

//判断最终结果，总之就是一个很巧妙的方法
(n < 0) ? 1 : (n >= MAXIMUM_CAPACITY) ? MAXIMUM_CAPACITY : n + 1;

对于构造方法4：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
public HashMap(Map<? extends K, ? extends V> m) {
	this.loadFactor = DEFAULT_LOAD_FACTOR;
	putMapEntries(m, false);
}

final void putMapEntries(Map<? extends K, ? extends V> m, boolean evict){
	int s = m.size();
	if (s > 0) {
		if (table == null) { // 如果桶还未初始化
			//计算桶的大小
			float ft = ((float)s / loadFactor) + 1.0F;//+1.0F的作用是为了减少扩容次数
			int t = ((ft < (float)MAXIMUM_CAPACITY) ?
			        (int)ft : MAXIMUM_CAPACITY);
			if (t > threshold) //重新赋值
			   threshold = tableSizeFor(t);
		}
		else if (s > threshold) //否则判断当前哈希桶是否能存下m中所有元素
			resize(); //不能则扩容
		for (Map.Entry<? extends K, ? extends V> e : m.entrySet()) {
			K key = e.getKey();  //拷贝元素
			V value = e.getValue();
			putVal(hash(key), key, value, false, evict);
		}
	}
}

成员方法

定位目标哈希桶static final int hash(Object key)

定位到目标哈希桶是很关键的第一步，只有定位找到位置后才能做下一步操作。很显然，我们希望HashMap里面的元素位置尽量分布均匀，因为如果很多元素都堆叠在某一个位置，那么我们定位到哈希桶后，还需要继续遍历该位置下的链表或者红黑树，导致效率降低，所以应尽量使得每个哈希桶内的元素只有一个，那么当我们用hash算法求得这个位置的时候，马上就可以知道对应位置的元素就是我们要的，而不用遍历链表或者红黑树，大大优化了查询的效率。HashMap定位数组索引位置，直接决定了hash方法的离散性能。下面是定位哈希桶的源码：

1
2
3
4
5
6
7
8
9
static final int hash(Object key) { // 计算key的hash值
    int h;
    // 得到key对象的hashCode值
    // 将hashCode与其右移16位后的数进行异或运算
    return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
int n = tab.length;
// 将(tab.length - 1) 与 hash值进行&运算
int index = (n - 1) & hash;
分析

对于任意给定的对象，只要它的hashCode()返回值相同，那么计算得到的hash值总是相同的。我们首先想到的就是把hash值对table长度取模运算，这样一来，元素的分布相对来说是比较均匀的。

但是模运算消耗还是比较大的，而计算机比较快的运算为位运算，因此上述源码中选择位运算代替模运算。

这个有个设置非常巧妙：它通过(table.length -1) & h来得到该对象的索引位置，这个优化是基于以下公式：x mod (2^n) = x & (2^(n - 1))。这就解释了HashMap底层数组的大小为什么总是2的次方，为了让位运算的离散效果达到与模运算一致，以至于尽量降低发生哈希冲突的概率，尽量把数据分配均匀，尽量提高HashMap的存取效率。

代码中计算hash值时用到(h = key.hashCode()) ^ (h >>> 16)，将hashCode的高 16位与hashCode进行异或运算，主要是为了在的数组大小较小的时候，让高位也参与运算，并且不会有太大的开销，而让高位也参与计算，目的也是为了降低发生哈希冲突的概率。

向表中添加键值对public V put(K key, V value)

整个过程大致如下：

  1. 先通过哈希值计算出key映射到哪个桶；
  2. 如果桶上没有碰撞冲突，则直接插入；
  3. 如果遇上了冲突，则需要冲突处理：
    （1）如果该桶使用红黑树处理冲突，则调用红黑树的方法插入数据；
    （2）否则采用传统的链式方法插入。如果链的长度达到临界值，则把链转变为红黑树；
  4. 如果桶中存在重复的键，则用新值替换老值并返回老值；
  5. 如果size大于阈值threshold，则进行扩容。
1
2
3
public V put(K key, V value) {
    return putVal(hash(key), key, value, false, true);
}

不难发现核心方法是putVal方法，即final V putVal(int hash, K key, V value, boolean onlyIfAbsent,boolean evict)，主要参数及含义如下：

  • hash：key的哈希值；
  • key：要存储的key；
  • value：要存储的值；
  • onlyIfAbsent：true代表不更改现有的值，否则覆盖；
  • evict：如果为false表示table为创建状态

源码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
    Node<K,V>[] tab; //存储table的引用 
    Node<K,V> p; int n, i; //n为桶的个数，i为目标桶的下标
    //(tab = table) == null如果是第一次插入，则一定为null
    //或者桶的个数为0，对table进行初始化
    if ((tab = table) == null || (n = tab.length) == 0) 
        n = (tab = resize()).length; //初始化完成后赋值n
    //将目标桶下第一个元素赋值给p，若p == null，则代表目标桶还未存储过元素，直接初始化桶并插入即可
    if ((p = tab[i = (n - 1) & hash]) == null) 
        tab[i] = newNode(hash, key, value, null);
    else { //否则说明发生哈希冲突
        Node<K,V> e; K k;
        //如果桶下第一个元素的键与要插入的键重复，则用value覆盖老值
        if (p.hash == hash && ((k = p.key) == key || (key != null && key.equals(k))))
            e = p;
        else if (p instanceof TreeNode)//否则往下插入，此情况下说明桶下存储结构为红黑树，树节点插入
            e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
        else { //否则存储结构为链表，链表遍历判断插入
            for (int binCount = 0; ; ++binCount) { //计数器代表当前为桶下链表中的第几个元素
                if ((e = p.next) == null) {//若遇到null，直接插入节点
                    p.next = newNode(hash, key, value, null);
                    //判断此时链表长度是否达到转化红黑树的阈值
                    if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
                        treeifyBin(tab, hash);//若是则进行转化
                    break;
                }
                //若找到键相同节点，则进行覆盖
                if (e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k))))
                    break;
                p = e;
            }
        }
        //此情况代表，插入键值对是进行了覆盖操作，此时返回被覆盖的值
        if (e != null) { // existing mapping for key
            V oldValue = e.value;
            if (!onlyIfAbsent || oldValue == null)
                e.value = value;
            afterNodeAccess(e); // 访问后回调
            return oldValue;
        }
    }
    ++modCount;
    if (++size > threshold) //如果此时表中元素个数大于阈值threshold，则进行扩容，
        resize();
    afterNodeInsertion(evict); //插入后回调
    return null;
}

移除键值对public V remove(Object key)

从下述代码中不难发现与上述put方法有些类似，这里重复的地方不过多赘述，主要步骤：

  1. 先找到元素的目标桶，即存储位置；
  2. 如果该桶下的存储结构是链表的话，则遍历找到并删除即可；
  3. 如果是红黑树结构，则遍历找到并删除，如果此时节点数少于红黑树转链表的阈值6时，调用untreeify方法将红黑树转化成链表。
1
2
3
4
5
public V remove(Object key) {
    Node<K,V> e;
    return (e = removeNode(hash(key), key, null, false, true)) == null ?
        null : e.value;
}

主要分析一下核心方法final Node<K,V> removeNode(int hash, Object key, Object value, boolean matchValue, boolean movable)：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
final Node<K,V> removeNode(int hash, Object key, Object value, boolean matchValue, boolean movable) {
 Node<K,V>[] tab; Node<K,V> p; int n, index;
 //前半部分为找到目标节点
 if ((tab = table) != null && (n = tab.length) > 0 &&
     (p = tab[index = (n - 1) & hash]) != null) {//先定位到目标桶中
     Node<K,V> node = null, e; K k; V v;
     if (p.hash == hash &&
         ((k = p.key) == key || (key != null && key.equals(k)))) //如果目标桶中第一个元素为要删除的目标元素，则赋值geinode
         node = p;
     else if ((e = p.next) != null) { //判断该桶下的其他元素
         if (p instanceof TreeNode) //若元素为树节点，则调用方法去树中查询，查询结果赋值给node
             node = ((TreeNode<K,V>)p).getTreeNode(hash, key);
         else { //否则即为链表结构
             do {  
                 if (e.hash == hash &&
                     ((k = e.key) == key ||
                      (key != null && key.equals(k)))) {
                     node = e; //找到节点则赋值给node并break
                     break;
                 }
                 p = e;
             } while ((e = e.next) != null);
         }
     }
     //接下来对于找到的节点从哈希表中删除
     if (node != null && (!matchValue || (v = node.value) == value ||
                          (value != null && value.equals(v)))) {
         if (node instanceof TreeNode) //是树节点的话，则调用树节点的删除方法
             ((TreeNode<K,V>)node).removeTreeNode(this, tab, movable);
         else if (node == p) //代表要删的是桶下第一个元素
             tab[index] = node.next; //将下一个元素赋值给桶
         else
             p.next = node.next; //否则直接链表删除
         ++modCount;
         --size; 
         afterNodeRemoval(node);
         return node;
     }
 }
 //无目标元素则返回null
 return null;
}

获取元素public V get(Object key)

获取元素的方法相对上述两个方法而言更加简单，而且核心方法final Node<K,V> getNode(int hash, Object key)与上述final Node<K,V> removeNode(int hash, Object key, Object value, boolean matchValue, boolean movable)方法的前半部分重合度很高，就不展开细讲了。

1
2
3
4
public V get(Object key) {
   Node<K,V> e;
    return (e = getNode(hash(key), key)) == null ? null : e.value;
}

将链表转换为红黑树final void treeifyBin(Node<K,V>[] tab, int hash)

在上述putVal方法中，添加完节点后，如果当前桶中链表长度大于8时调用，代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
//判断此时链表长度是否达到转化红黑树的阈值
if (binCount >= TREEIFY_THRESHOLD - 1) // -1 for 1st
    treeifyBin(tab, hash);//若是则进行转化

//treeifyBin
final void treeifyBin(Node<K,V>[] tab, int hash) {
    int n, index; Node<K,V> e;
    //由putVal传入的tab必然部位null，直接看后面一个条件
    //当tab.length < MIN_TREEIFY_CAPACITY = 64时，即当表中桶的数量太小、不足64个时，我们选择扩容
    if (tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY)
        resize();
    else if ((e = tab[index = (n - 1) & hash]) != null) { //否则将链表转换为红黑树
    	//先用e定位到链表的第一个节点
        TreeNode<K,V> hd = null, tl = null; //构建红黑树
        do {
        	//将原节点转化成树节点
            TreeNode<K,V> p = replacementTreeNode(e, null);
            if (tl == null) //赋值头结点
                hd = p;
            else { //进行连接
                p.prev = tl;
                tl.next = p;
            }
            tl = p;
        } while ((e = e.next) != null);
        //不难发现上述while虽然是一颗红黑树，但是是链状的
        if ((tab[index] = hd) != null) //将红黑树头节点放进桶中
            hd.treeify(tab); //将上述链状红黑树进行平衡处理
    }
}

之后treeify红黑树的平衡处理不再细讲，总结一下上述链表转化成红黑树的步骤：

  1. 根据哈希表中元素个数确定是扩容还是树形化；
  2. 如果是树形化遍历桶中的元素，创建相同个数的树形节点，复制内容，建立起联系；
  3. 然后让桶中的第一个元素指向新创建的树根节点，替换桶的链表内容为树形化内容；
  4. 最后处理红黑树，红黑树中比较大小的依据为hash值。

哈希表的扩容，final Node<K,V>[] resize()

扩容时机：（每次扩容都将哈希表大小扩容成原来的两倍）

  • 当容器中的元素数量大于阈值（即加载因子乘以哈希表大小）；
  • 当某哈希桶中元素数量大于8，且哈希表带下即桶的个数小于64时。

在分析源代码之前我们先分析一下扩容的过程：

  1. 首先计算扩容后的哈希表的大小（哈希桶数量）及阈值（最大容量）；
  2. 然后再将原哈希表中元素重新计算目标桶并放入目标桶值（即rehash）。

显然第1步无法优化，但是对于第2步这里有一个很巧妙的优化，假设rehash时我们重新开始计算，这是十分耗时的，根据位运算的性质，我们先看下面这一个例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
假设我们要转移的元素的hash值为：
hash1:1111 1111 1111 1111 0000 1111 0000 0101
hash2:1111 1111 1111 1111 0000 1111 0001 0101
扩容前，假设哈希表大小 n = 16
n = 16		0000 0000 0000 0000 0000 0000 0001 0000
n - 1 = 15	0000 0000 0000 0000 0000 0000 0000 1111
hash1:		1111 1111 1111 1111 0000 1111 0000 0101
-------------------------------------------------------- &运算
index1 = 5	0000 0000 0000 0000 0000 0000 0000 0101

n - 1 = 15	0000 0000 0000 0000 0000 0000 0000 1111
hash2:		1111 1111 1111 1111 0000 1111 0001 0101
-------------------------------------------------------- &运算
index2 = 5	0000 0000 0000 0000 0000 0000 0000 0101

========================================================
扩容后，哈希表大小 n = 16 * 2 = 32
n = 32		0000 0000 0000 0000 0000 0000 0010 0000
n - 1 = 31	0000 0000 0000 0000 0000 0000 0001 1111
hash1:		1111 1111 1111 1111 0000 1111 0000 0101
-------------------------------------------------------- &运算
index1 = 5	0000 0000 0000 0000 0000 0000 0000 0101

n - 1 = 31	0000 0000 0000 0000 0000 0000 0001 1111
hash2:		1111 1111 1111 1111 0000 1111 0001 0101
-------------------------------------------------------- &运算
index2 = 21	0000 0000 0000 0000 0000 0000 0001 0101

我们不难发现，由于每次扩容是将哈希表大小翻倍，及n * 2，在二进制上的体现是左移一位，则n - 1的二进制为则相当于在原二进制上左边多一个1，并不影响原先相与的结果，仅仅只影响一位，而当哈希值值的这一位为0时，则扩容后的目标桶不发生改变，而为1时则相当于目标桶从i移向了i + oldN（即右移原素组大小），综上：扩容后，节点要么就在原来的位置，要么就被分配到”原位置+旧容量“这个位置。有上述的结论，即可提高rehash的效率。

下图为扩容前后哈希表的变化：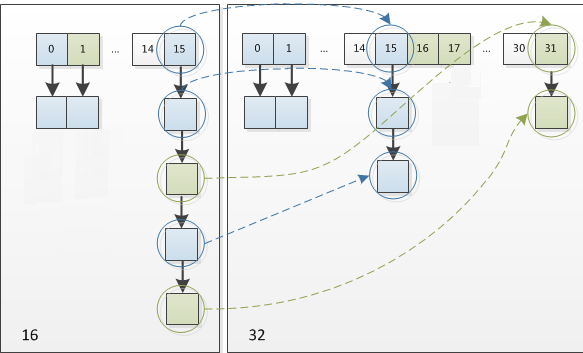
在这里插入图片描述
很明显，减小了哈希冲突的次数，正是因为这样巧妙的rehash方式，既省去了重新计算哈希值的时间，而且同时，由于新增的1bit是0还是1可以认为是随机的，在resize的过程中保证了rehash之后每个桶上的节点数一定小于等于原来桶上的节点数，保证了rehash之后不会出现更严重的哈希冲突，均匀的把之前的冲突的节点分散到新的桶中了。

加下来便是源码分析：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
final Node<K,V>[] resize() {
    Node<K,V>[] oldTab = table; //存下原哈希表
    int oldCap = (oldTab == null) ? 0 : oldTab.length; //记录原哈希表的大小
    int oldThr = threshold; //记录原阈值
    int newCap, newThr = 0; //扩容后大小和阈值
    if (oldCap > 0) {//如果原哈希表大小大于0
        if (oldCap >= MAXIMUM_CAPACITY) { //判断其是否超过了上限
            threshold = Integer.MAX_VALUE;
            return oldTab;
        }	//判断扩容为原先两倍后有没有超出上限
        else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
                 oldCap >= DEFAULT_INITIAL_CAPACITY)
            newThr = oldThr << 1; // double threshold
    }	//原哈希表大小为0，但是阈值大于0，此时便是之前提到的修正位置
    else if (oldThr > 0) // initial capacity was placed in threshold
        newCap = oldThr; //赋值给新大小
    else { //否则使用默认大小16和默认加载因子0.75计算出的阈值12              // zero initial threshold signifies using defaults
        newCap = DEFAULT_INITIAL_CAPACITY;
        newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
    }
    if (newThr == 0) { //计算新阈值，即哈希表大小 * 加载因子
        float ft = (float)newCap * loadFactor;
        newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
                  (int)ft : Integer.MAX_VALUE);
    }
    threshold = newThr; //赋值
    @SuppressWarnings({"rawtypes","unchecked"})
    Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap]; //建立新哈希表
    table = newTab;
    if (oldTab != null) { //哈希表非空
        for (int j = 0; j < oldCap; ++j) { //遍历原哈希表中的每一个桶，将其移动至新哈希表
            Node<K,V> e;
            if ((e = oldTab[j]) != null) { //当前桶中有元素，并赋值给节点e
                oldTab[j] = null;  //便于最后原哈希表的置空和回收
                if (e.next == null) //当前桶只有一个元素
                    newTab[e.hash & (newCap - 1)] = e; //直接放进新位置中
                else if (e instanceof TreeNode) //如果是红黑树结构，则调用相关方法把树分开
                    ((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
                else { // preserve order 否则就是链表了，
                	//根据上述位运算结论，原链表的分解只可能成为两条链表
                    Node<K,V> loHead = null, loTail = null; //声明两条链表l和h
                    Node<K,V> hiHead = null, hiTail = null;
                    Node<K,V> next;
                    do { //用循环将所有节点取出并放入l或h中
                        next = e.next;
                        if ((e.hash & oldCap) == 0) { //这里就是提高效率的地方，只需比较一位二进制为即可判断它在新哈希表中的目标桶位置
                        //为0代表位置不变
                            if (loTail == null)	
                                loHead = e;
                            else
                                loTail.next = e;
                            loTail = e;
                        }
                        else { //为1则代表变为 原位置+旧容量
                            if (hiTail == null)
                                hiHead = e;
                            else
                                hiTail.next = e;
                            hiTail = e;
                        }
                    } while ((e = next) != null);
                    if (loTail != null) { //将两条链表分别放进哈希桶中
                        loTail.next = null;
                        newTab[j] = loHead;
                    }
                    if (hiTail != null) {
                        hiTail.next = null;
                        newTab[j + oldCap] = hiHead;
                    }
                }
            }
        }
    }
    return newTab;
}

这里再简单描述一下关于桶中元素为红黑树的情况：

1
2
else if (e instanceof TreeNode) //如果是红黑树结构，则调用相关方法把树分开
	((TreeNode<K,V>)e).split(this, newTab, j, oldCap);

split方法是先将当前这棵树按照上述位运算结论，分解成类似上述l、h两条链表的l、h两颗红黑树，然后分别对两颗红黑树进行节点数量判断，若小于UNTREEIFY_THRESHOLD（红黑树转链表的阈值），则将其转变成链表，然后分别存储新哈希表的目标桶中。

扩展

HashMap初始化时，推荐使用指定集合初始值大小的构造方法，即使用HashMap(int initialCapacity)进行初始化，为的是减少扩容次数，扩容操作十分耗时。

$初始容量 = \frac{需存储元素个数}{加载因子} + 1$

注意加载因子（即 loaderfactor）默认为 0.75，如果暂时无法确定初始值大小，请设置为 16（即默认值）。